1 Statics

Mechanics is the branch of physics and engineering concerned with the behavior of bodies under the action of forces, encompassing statics and dynamics. This chapter introduces statics, the study of bodies in equilibrium where net forces and moments are zero. We examine balanced force systems, including space and vector diagrams, conditions of equilibrium, and the calculation of resultant forces and moments.

1.1 Space Diagrams

A space diagram illustrates the geometry of the system and the applied forces.

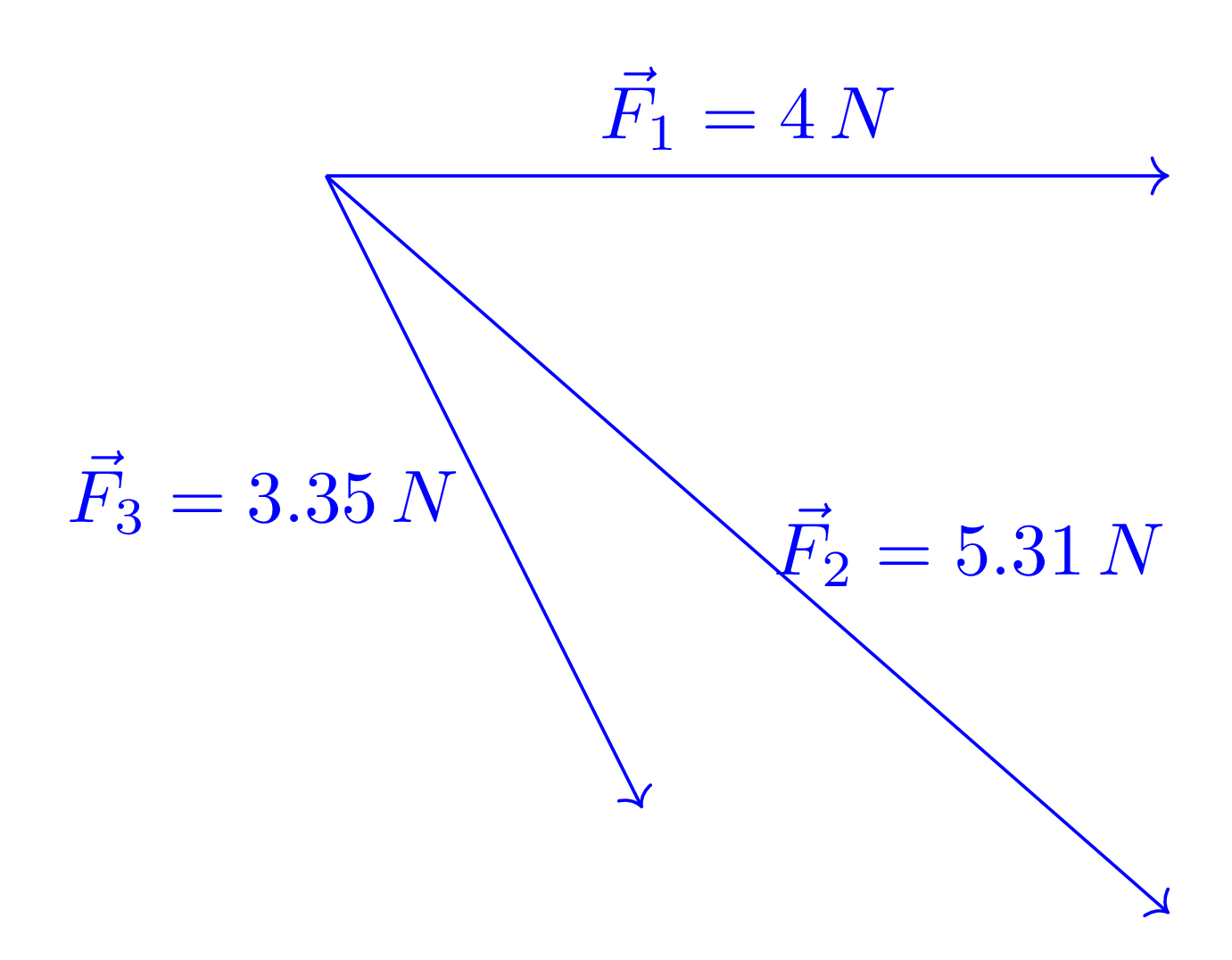
1.2 Vector Diagrams

A vector diagram (or force polygon) is a scaled graphical construction in which force vectors are placed head-to-tail in succession. It is used to determine the resultant of a system of forces through vector addition, as well as to resolve equilibrium problems when the polygon closes.

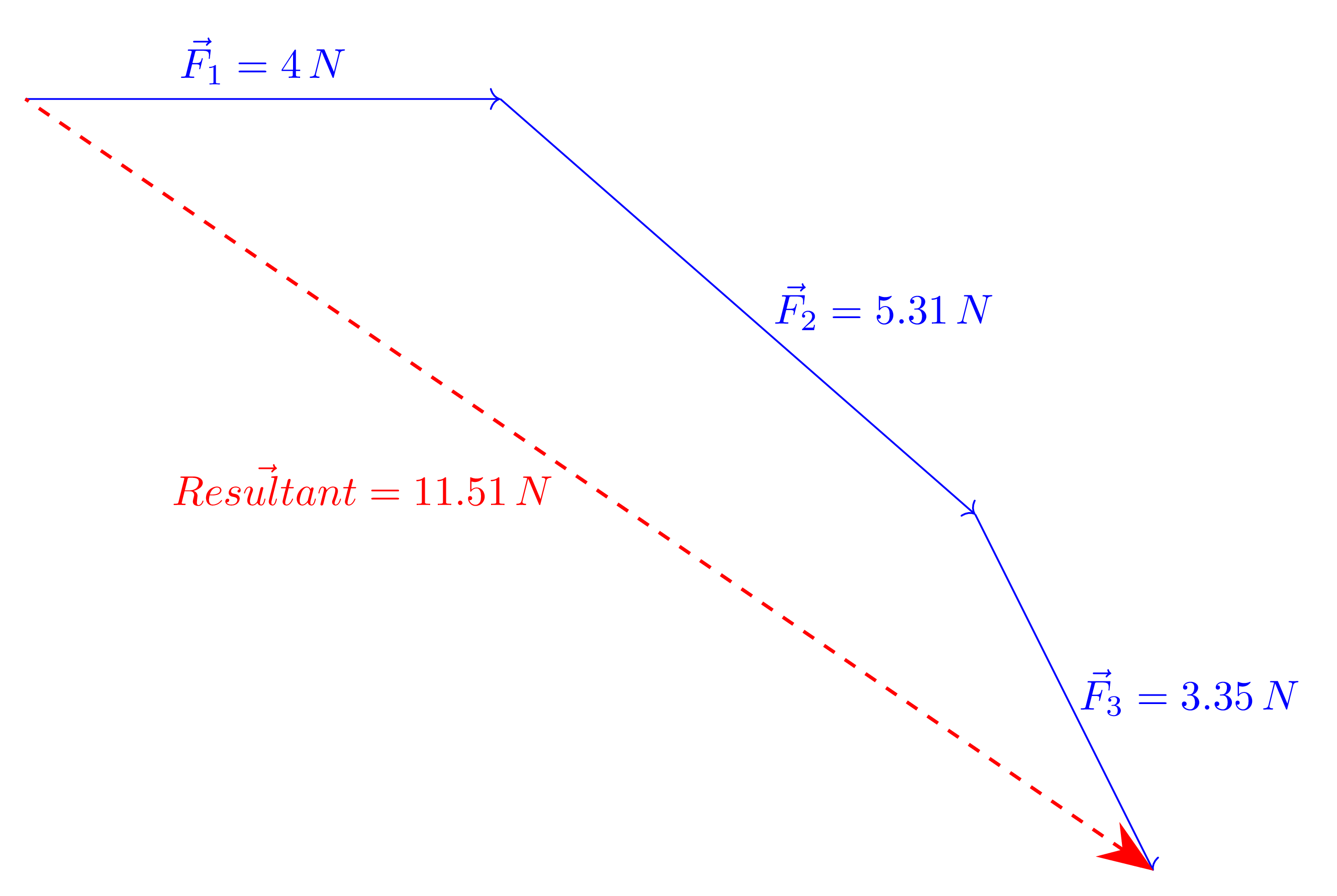
1.2.1 Resultant

The resultant is a single force that has exactly the same effect on an object as all the original forces acting together. It is found by adding the forces vectorially taking into account both their magnitude and direction. The resultant gives the overall direction and magnitude of the combined forces as shown in Figure 1.2.

1.2.2 Equilibrium

Equilibrium of an object occurs when all the forces acting on it are balanced, so the object remains at rest or moves at a constant speed in a straight line. In equilibrium, as shown in Figure 1.3, there is no net force or acceleration, meaning the object is in a stable state without any change in its motion.

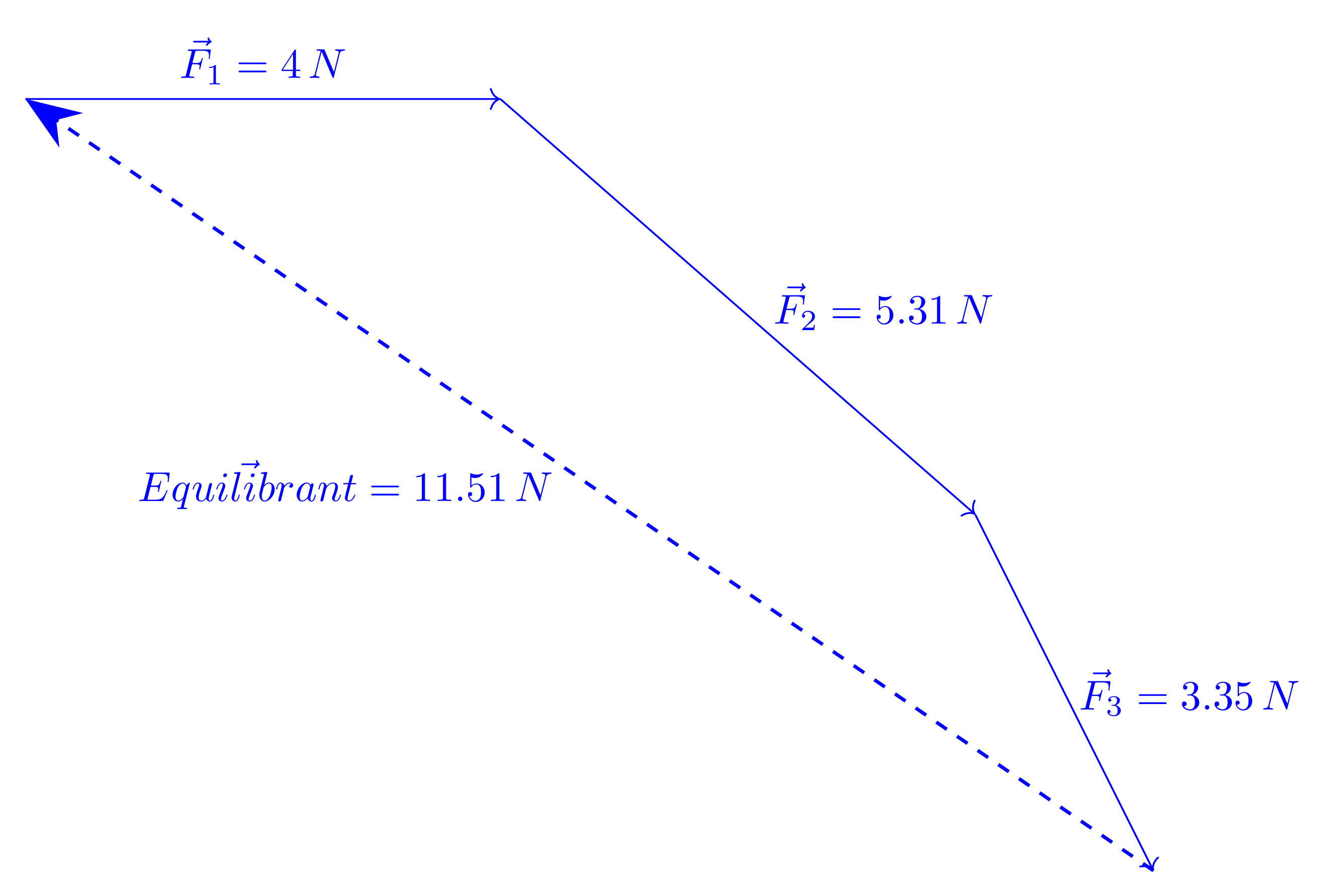
1.3 Conditions of Equilibrium

Net force must be zero:

\[ \sum_{k} \vec{F}_{k} = \vec{0} \tag{1.1}\]

Net torque must be zero:

\[ \sum_{k} \vec{\tau}_{k} = \vec{0} \tag{1.2}\]

1.4 Cosine Rule

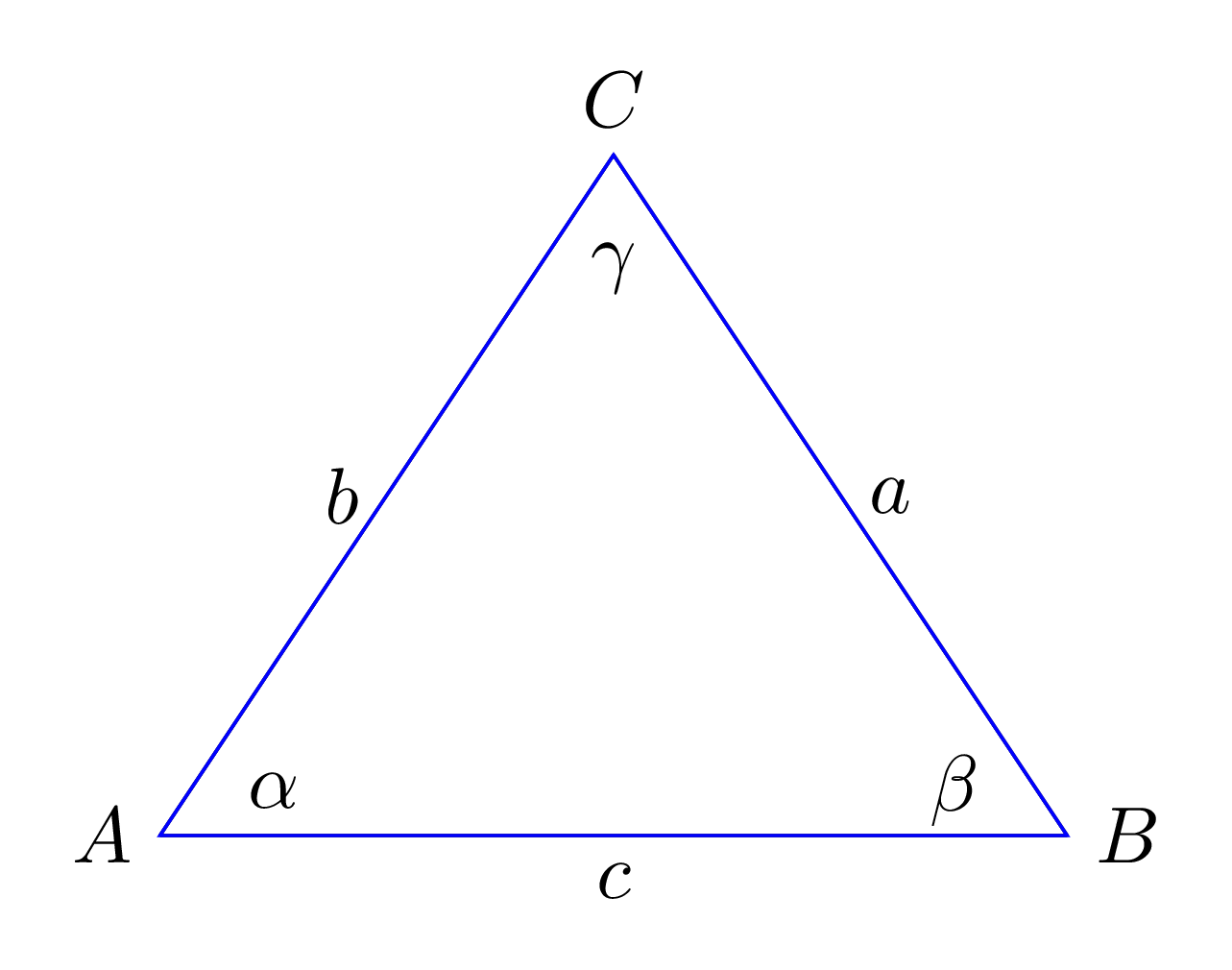
The Cosine Rule is used to relate the lengths of the sides of a triangle as shown in Figure 1.4 to the cosine of one of its angles:

\[ c^2 = a^2 + b^2 - 2ab\cos \gamma \tag{1.3}\]

Where:

a, b, c are the sides of the triangle.
\(\gamma\) is the angle opposite side c.

1.5 Sine Rule

The Sine Rule relates the sides and angles of a triangle in Figure 1.4:

\[ \frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma} \tag{1.4}\]

Where:

\(\alpha\), \(\beta\), \(\gamma\) are the angles of the triangle.
a, b, c are the sides of the triangle opposite to angles \(\alpha\), \(\beta\), \(\gamma\) respectively.

1.6 Problem Set

Example 1.1 Two slings of equal length are slung from a horizontal beam and connected to a ring at their lower ends, the slings and beam forming an equilateral triangle. Find the force in each sling when a load of 30 kN hangs from the ring.

Warning

In Python, the trigonometric functions in the math module (sin, cos, tan, etc.) expect angles in radians, not degrees. Always convert degrees to radians before using these functions.

"""
Sling Tension Calculator

Calculates the tension in each sling of a two-sling system
supporting a vertical load, the slings and beam forming 
an equilateral triangle.
"""

import math

# ====================================
# INPUT PARAMETERS
# ====================================

vertical_load_kn = 30  # Total vertical load in kilonewtons
sling_angle_degrees = 60  # Angle each sling makes with horizontal

# ====================================
# CALCULATIONS
# ====================================

# Convert angle from degrees to radians for trigonometric functions
sling_angle_radians = math.radians(sling_angle_degrees)

# Apply vertical equilibrium equation:
# Sum of vertical forces = 0
# 2 * T * sin(θ) = W
# where T is tension in each sling, θ is angle, W is vertical load
tension_per_sling_kn = vertical_load_kn / (2 * math.sin(sling_angle_radians))

# ====================================
# OUTPUT RESULTS
# ====================================

print(f"Tension in each sling: {tension_per_sling_kn:.4f} kN")

Example 1.2 Two identical slings of equal length are attached to a horizontal beam and meet at a ring from which a 45 kN load is suspended. The slings and the beam form an isosceles triangle in which each sling makes an angle of 50° with the horizontal. Find the force (tension) in each sling.

"""
Sling Tension Calculator

Calculates the tension in each sling of a two-sling system
supporting a vertical load, the slings and the beam form 
an isosceles triangle.
"""

import math

# ====================================
# INPUT PARAMETERS
# ====================================

vertical_load_kn = 45  # Total vertical load in kilonewtons
sling_angle_degrees = 50  # Angle each sling makes with horizontal

# ====================================
# CALCULATIONS
# ====================================

# Convert angle from degrees to radians for trigonometric functions
sling_angle_radians = math.radians(sling_angle_degrees)

# Apply vertical equilibrium equation:
# Sum of vertical forces = 0
# 2 * T * sin(θ) = W
# where T is tension in each sling, θ is angle, W is vertical load
tension_per_sling_kn = vertical_load_kn / (2 * math.sin(sling_angle_radians))

# ====================================
# OUTPUT RESULTS
# ====================================

print(f"Tension in each sling: {tension_per_sling_kn:.4f} kN")

Example 1.3 Two lifting ropes are connected at their lower ends to a common shackle from which a load of 25 kN hangs. If the ropes make angles of 32° and 42° respectively to the vertical, find the tension in each rope.

"""
Rope Tension Calculator (Law of Sines)

Calculates tensions in two ropes supporting a load using the law of sines.
The system forms a triangle where the angles and load are known.
"""

import math

# ====================================
# INPUT PARAMETERS
# ====================================

vertical_load_kn = 25  # Total vertical load in kilonewtons
angle_opposite_rope2_deg = 32  # Angle opposite to tension T2 (degrees)
angle_opposite_rope1_deg = 42  # Angle opposite to tension T1 (degrees)

# Calculate the third angle of the triangle (angles sum to 180°)
angle_opposite_load_deg = 180 - (angle_opposite_rope2_deg + angle_opposite_rope1_deg)

# ====================================
# CALCULATIONS
# ====================================

# Convert all angles from degrees to radians for trigonometric functions
angle_opposite_rope2_rad = math.radians(angle_opposite_rope2_deg)
angle_opposite_rope1_rad = math.radians(angle_opposite_rope1_deg)
angle_opposite_load_rad = math.radians(angle_opposite_load_deg)

# Apply the law of sines to find tensions:
# T1 / sin(θ1) = T2 / sin(θ2) = W / sin(θ3)
# where θ1 is opposite T1, θ2 is opposite T2, θ3 is opposite W

# Tension in rope 1 (opposite to angle_opposite_rope1)
tension_rope1_kn = (
    vertical_load_kn
    * math.sin(angle_opposite_rope1_rad)
    / math.sin(angle_opposite_load_rad)
)

# Tension in rope 2 (opposite to angle_opposite_rope2)
tension_rope2_kn = (
    vertical_load_kn
    * math.sin(angle_opposite_rope2_rad)
    / math.sin(angle_opposite_load_rad)
)

# ====================================
# OUTPUT RESULTS
# ====================================

print(f"Tension in rope 1: {tension_rope1_kn:.4f} kN")
print(f"Tension in rope 2: {tension_rope2_kn:.4f} kN")

Example 1.4 The angle between the jib and vertical post of a jib crane is 40°, and the angle between the jib and tie is 45°. Find the force in the jib and tie when a load of 15 kN hangs from the crane head.

"""
Jib and Tie Force Calculator

Calculates forces in a jib and tie member supporting a vertical load.
Uses the law of sines to solve the force triangle.
"""

import math

# ====================================
# INPUT PARAMETERS
# ====================================

vertical_load_kn = 15  # Total vertical load in kilonewtons
angle_jib_to_vertical_deg = 40  # Angle between jib and vertical (degrees)
angle_jib_to_tie_deg = 45  # Angle between jib and tie (degrees)

# Calculate the third angle in the force triangle (angles sum to 180°)
angle_tie_to_load_deg = 180 - angle_jib_to_vertical_deg - angle_jib_to_tie_deg

# ====================================
# CALCULATIONS
# ====================================

# Convert all angles from degrees to radians for trigonometric functions
angle_jib_to_vertical_rad = math.radians(angle_jib_to_vertical_deg)
angle_jib_to_tie_rad = math.radians(angle_jib_to_tie_deg)
angle_tie_to_load_rad = math.radians(angle_tie_to_load_deg)

# Apply the law of sines to find forces in jib and tie:
# F_jib / sin(θ_opposite_jib) = F_tie / sin(θ_opposite_tie) = W / sin(θ_ref)
# where the reference angle is the angle between jib and tie

# Force in jib (compression or tension depending on configuration)
force_jib_kn = (
    vertical_load_kn * math.sin(angle_tie_to_load_rad) / math.sin(angle_jib_to_tie_rad)
)

# Force in tie (tension)
force_tie_kn = (
    vertical_load_kn
    * math.sin(angle_jib_to_vertical_rad)
    / math.sin(angle_jib_to_tie_rad)
)

# ====================================
# OUTPUT RESULTS
# ====================================

print(f"Force in jib: {force_jib_kn:.4f} kN")
print(f"Force in tie: {force_tie_kn:.4f} kN")

Example 1.5 The lengths of the vertical post, jib, and tie of a jib crane are 8, 13, and 9 m, respectively. Find the forces in the jib and tie when a load of 20 kN hangs from the crane head.

"""
Structural Force Calculator

Calculates forces in a triangular structure (post, jib, tie) given the
member lengths and applied load. Uses law of cosines to find angles,
then law of sines to determine member forces.
"""

import math

# ====================================
# INPUT PARAMETERS
# ====================================

post_length_m = 8  # Length of post member in meters
jib_length_m = 13  # Length of jib member in meters
tie_length_m = 9  # Length of tie member in meters
applied_load_kn = 20  # Applied vertical load in kilonewtons

# ====================================
# ANGLE CALCULATIONS (LAW OF COSINES)
# ====================================

# Calculate angle opposite to post using law of cosines:
# cos(θ_p) = (J² + T² - P²) / (2·J·T)
angle_opposite_post_rad = math.acos(
    (jib_length_m**2 + tie_length_m**2 - post_length_m**2)
    / (2 * jib_length_m * tie_length_m)
)

# Calculate angle opposite to tie using law of cosines:
# cos(θ_t) = (J² + P² - T²) / (2·J·P)
angle_opposite_tie_rad = math.acos(
    (jib_length_m**2 + post_length_m**2 - tie_length_m**2)
    / (2 * jib_length_m * post_length_m)
)

# Calculate angle opposite to jib (angles in triangle sum to π radians)
angle_opposite_jib_rad = math.pi - angle_opposite_post_rad - angle_opposite_tie_rad

# ====================================
# FORCE CALCULATIONS (LAW OF SINES)
# ====================================

# Apply law of sines to find member forces:
# F_jib / sin(θ_jib) = F_tie / sin(θ_tie) = W / sin(θ_post)

# Force in jib member
force_jib_kn = (
    applied_load_kn
    * math.sin(angle_opposite_jib_rad)
    / math.sin(angle_opposite_post_rad)
)

# Force in tie member
force_tie_kn = (
    applied_load_kn
    * math.sin(angle_opposite_tie_rad)
    / math.sin(angle_opposite_post_rad)
)

# ====================================
# CONVERT ANGLES TO DEGREES FOR OUTPUT
# ====================================

angle_opposite_post_deg = math.degrees(angle_opposite_post_rad)
angle_opposite_tie_deg = math.degrees(angle_opposite_tie_rad)
angle_opposite_jib_deg = math.degrees(angle_opposite_jib_rad)

# ====================================
# OUTPUT RESULTS
# ====================================

print(f"theta_p = {angle_opposite_post_deg:.4f} degrees")
print(f"theta_t = {angle_opposite_tie_deg:.4f} degrees")
print(f"theta_j = {angle_opposite_jib_deg:.4f} degrees")
print()
print(f"Force in jib (F_J): {force_jib_kn:.4f} kN")
print(f"Force in tie (F_T): {force_tie_kn:.4f} kN")